The Flower Box

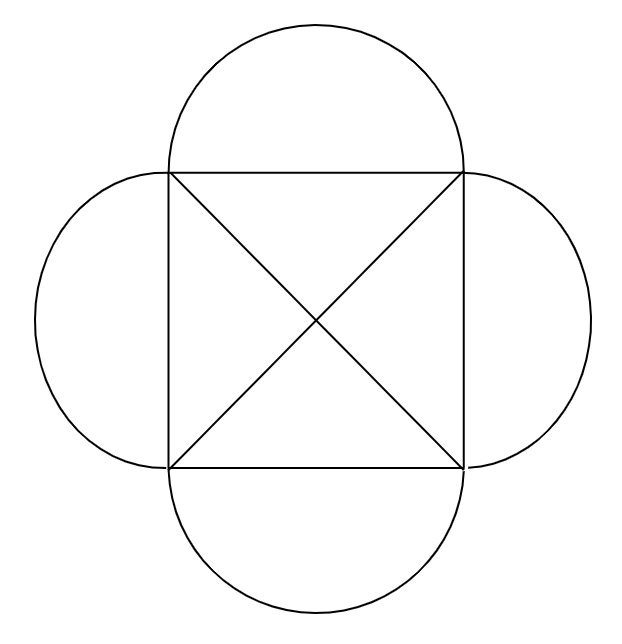
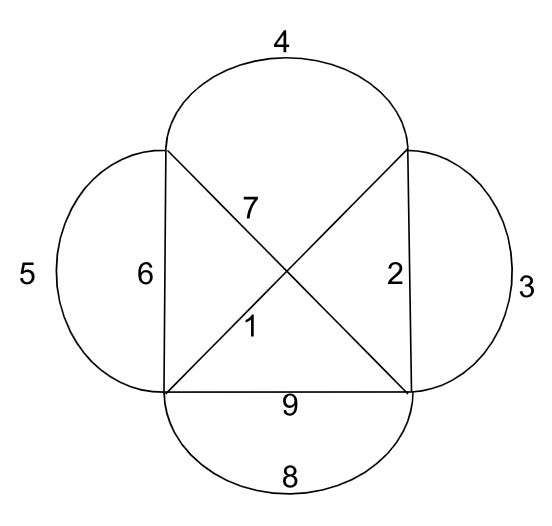
When I was 10 years old, my family and I were driving up to the Ozarks for a camping trip. Tired of my constant boredom sighs and “are we there yet”s, my mom drew a shape on a piece of paper:

“Try to draw this exact shape, but you’re only allowed to touch your pen to the paper once, and you can’t retrace any lines.”

If you’ve never seen this puzzle before, I encourage you to go try it. Seriously! And you know what, even if you have seen it before and know the answer I want you to go and try drawing it anyway. Go get out a notebook and try drawing the shape out a little bit. Don’t worry, I’ll wait. Here, you can subscribe while I wait.

….

….

….

Did you try it? Here’s what I predict a number of you did:

1. Most of you probably ignored my request to draw it by having some silly excuse like being too busy at work or being in the bathroom.

2. A few of you may have actually tried it and gotten kind of close, but not quite completing it. This group is probably lining up in the “It’s impossible” camp.

3. A smaller number of you might have gotten really close, maybe just one edge away, and you feel like you’re not quite ready to throw in the towel, but you’re not really sure how to proceed either.

Instead of telling you the solution I’ll just tell you what 10 year old Rohan did. I worked for weeks on this puzzle. I tried starting from every corner, from the middle of the crossing edges, drawing arcs and shapes all over the place. When I ran out of paper I started using the spare napkins in the car. After our trip I would draw the shape on the shower glass over and over hoping that I had missed something silly. I would draw the shape on my arm before sleeping, I would take my sister’s gel pens and draw it on her beloved coloring books, I’d draw the shape on my plate when finishing up dinner, but no matter how hard I tried, I could not replicate it.

I asked my mom one day:

Me: Is this puzzle impossible?

Mom: I’m not sure, maybe it is.

Me: If I solve it, do you think I’ll win a million dollars?

Mom: You know, I’m sure you’ll get a prize of some kind. Now stop drawing on your sister’s arm.

---

Something about puzzles hooks us as humans. There’s something magical about getting absolutely obsessed by a well-crafted puzzle, something that keeps you on the brink between throwing your hands up and declaring it impossible vs. having some semblance of an answer. A puzzle with consistent constraints gives us a kind of toy universe to explore: the rules are laid out explicitly, and especially when the rules are simple to explain, (maybe even elegant), it’s especially rewarding to explore.

I was fortunate as a kid to have parents who gave me puzzles to work on. I wasn’t particularly great at arithmetic, memorization, or really just paying attention to my teachers in general, but I loved to play games and solve puzzles. It took a while, but eventually mathematics started to become really interesting to me when I started to learn higher math in high school. Even though we were introduced to the notion of “proofs” in Geometry, they felt very mechanical to me until we started seeing them in Calculus.

I realized later that the same muscle I had honed in puzzle-solving from an early age served me well in my mathematical endeavors. A lot of the best kind of mathematics is like puzzle-solving: working within some constraints, and exploring patterns. And like puzzle-solving, there was always more than one way of going about an interesting problem.

But as I continued to learn more and more advanced math, I saw more and more of my friends and classmates lose interest and question why anyone in their right mind would want to learn more math after high school. “When will we ever need to actually use derivatives? If my graphing calculator can plot these functions, what’s the point in us learning how to?”

At the time I didn’t really have a good answer for any of these complaints. Something told me that there was something we might be collectively missing, but intuitively I knew that math wasn’t nearly as useful in daily life as we had been taught.

That’s because…

Math is Art

I don’t mean that in a trite or superficial way. I don’t mean that math is like art or that math is beautiful like some art — I mean that math is art. G.H. Hardy (the famous mathematician Srinivasa Ramanujan’s advisor) summed it up in a pithy statement:

A mathematician, like a painter or poet, is a maker of patterns. If his patterns are more permanent than theirs, it is because they are made with ideas.

The problem, and fundamental reason why it’s hard for us to think of math as an art form, like music, painting, or writing, is because math happens to be something that happens to produce a lot of economic value. Because of this, math in our school system is architected to produce students who don’t necessarily enjoy math, but instead know how to use it in a “productive” manner. Like calculating sums or doing your taxes.

Imagine if we taught other art forms to young children like we do with math:

1. Music: “No no, you can’t just make up songs, you need to first learn structured music theory, how to read sheet music, and have memorized the circle of fifths. Otherwise the songs you make up would be atrocious!”

2. Drawing: “You can’t just draw whatever you like! You have to first learn how to properly draw many typical objects from various perspectives. Then after learning some proper compositional theory will you be allowed to draw freely, perhaps once you have an advanced graduate degree.”

3. Dance: “Make up your own dance?! That’s ludicrous! When have you ever seen anyone dance something entirely made up on their own?”

Maybe a few of you might even feel like our current education in the arts does feel a lot like the examples above (and if so I am deeply sorry for our state of the world). I believe this kind of tendency to limit creativity is rooted in our propensity to over-objectify reality; especially when art is naturally subjective.

For example, is there a best way to draw a bird? What would it be? If you had to imagine the best drawing of a bird you could, what would it look like?

Here are some birds I had a few folks (or AI) draw:

ChatGPT draws a bird

Rohan draws a bird in flight

Maya (age 2) draws a bird

Which one of these birds is “the best” bird? Which of these birds do you like best? What even are birds?

I’d argue that each of the pieces offers something. ChatGPT’s bird feels like a photorealistic depiction of a bird, but it also feels like the bird isn’t really alive. Kind of like a stuffed bird you might find in a museum exhibit or in a taxidermy studio.

For my bird I went with a more minimalist approach, capturing the bird in flight, and very far away. So far away that I wouldn’t have to draw any bird-y details and expose myself as a horrible drawer.

I’m certainly biased, but I really love Maya’s bird. I think it feels like a bird in a way that the other two don’t really capture. It also feels a bit like her own sense of self captured and entangled with the drawing.

So how is math anything like this? For that, let’s bring up the original puzzle.

The puzzle was to draw the figure:

without lifting up the pen from the paper and without retracing any lines. Let’s walk through some answers to the puzzle:

The Official “Answer”

It’s impossible. You can show this by isomorphically mapping the puzzle to a graph with 4 vertices and 10 edges. An unbroken chain of edges (an Eulerian trail) can only be constructed on a graph with exactly 0 or 2 vertices of odd degree. As there are 4 vertices of odd degree in this graph, this implies that no Eulerian trail exists.

How did this answer feel to you? To me, it felt a bit sterile. If you have some background in graph theory, you might really like this answer though!

Another “Answer”

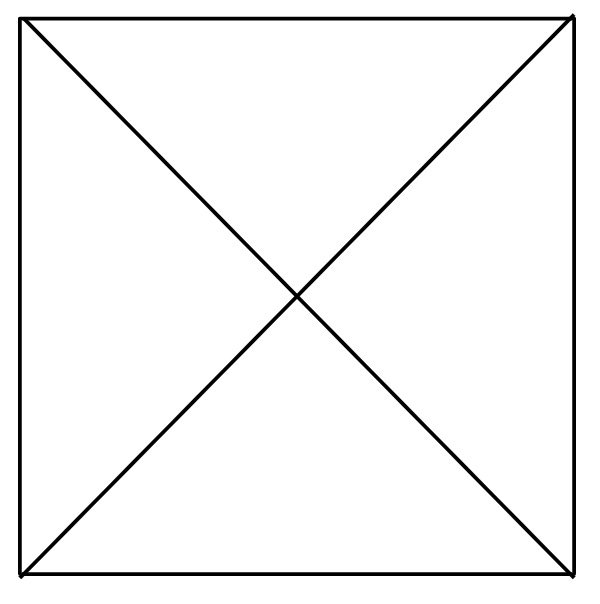
Sneaky, sneaky. Lifting the problem into a higher dimension. Was this satisfying? It felt like a nice “out of the box” solution to the puzzle, but it also played loose with the constraints a bit. Did this answer feel better than the first one though?

10 year old Rohan’s “Answer”

After playing with the puzzle more, I started to realize something. I would get to a place where I would have just one edge left to draw, but I couldn’t do it because my pen was on the other side and I’d have to retrace it. I asked myself a question:

“If someone were to remove any of the edges, would I be able to retrace it?”

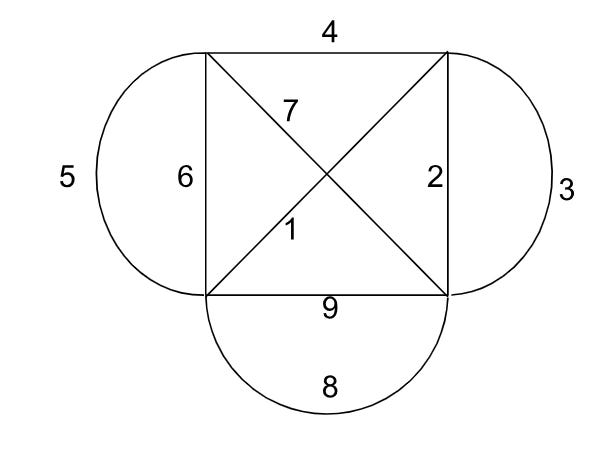
I realized that if I could draw this pattern (I included the edge order so you can see how I did it):

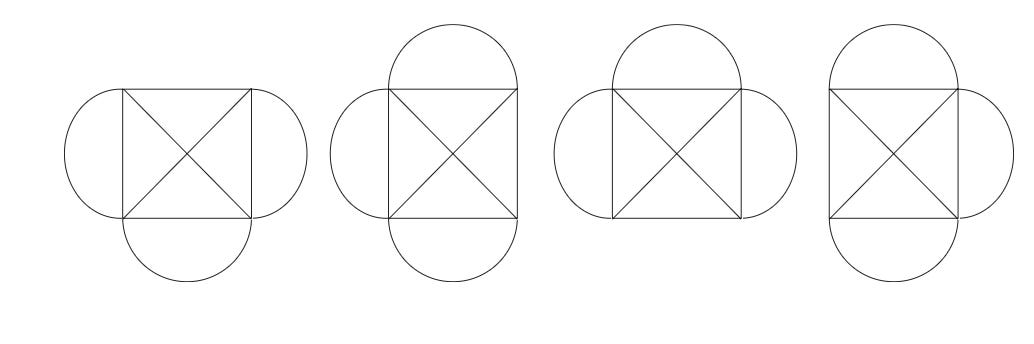
Then I could also draw all of these patterns:

by “rotating” the puzzle into the right orientation and starting from the right place again. I also realized that if I could draw these, I could also do:

Because there didn’t really seem to be a “difference” between the petal edges and the straight box edges. In other words, if I “swapped” a petal edge with its neighboring box edge, it wouldn’t really change the puzzle.

What I also realized was that this sort of “sameness” between the petal edges and the straight box edges meant that a simpler version of the problem could let me solve the harder one:

Because if a solution to this one existed, I could just “add back” the petals (no matter which corner I ended up on) and I’d be all done. But the interesting thing was that this problem seemed much simpler! I could enumerate all of the possible solutions and verify that nothing would actually work, and therefore the original puzzle was also impossible.

Whose was Best?

Which of these did you like the most? Maybe you liked all of the answers, but different aspects of each one were intriguing for different reasons. For example, the “official” answer is nice because there’s a hint of generalizability. You can broadly apply what it’s saying to all sorts of other puzzles (e.g. The Seven Bridges of Könisberg) on addition to this one.

I’m a bit biased, but I really liked 10 year old Rohan’s solution. It’s especially fun to see my thought process in hindsight, because even though I didn’t have any advanced mathematical terminology, I was touching on concepts like symmetry, group isomorphisms, and topological properties. But it didn’t really matter. It’s kind of like how Maya doesn’t need to know color composition theory to be able to intuit color, shape, and texture. She just kind of…does it. This is what math can and should be too.

As we get older, we learn to bury our naturally creative inclinations in favor of “optimized” ones, but this only dulls our relationship with the wider world and with ourselves. Math doesn’t have to be something we just use for productivity. Like any art form, we can also find it rewarding because it’s just fun to do.

Does math as an art sound really difficult or impossible to you? Did you grow up learning math meant rote memorization, reading arcane proofs, trying to understand Euler’s number by learning interest rates, and working on inane PEMDAS problems? If you’re interested, I’d love to chat on finding ways to make math more accessible as an art form. I, for one, will be giving my kids a ton of puzzles and seeing what they come up with.

Also, please read Paul Lockhart’s beautiful essay: A Mathematician’s Lament, from which nearly all of my feelings on the subject originate from. Have a wonderful week.